ABC, H. (2005).
Digit symbol substitution test - operations manual.
https://healthabc.nia.nih.gov/sites/default/files/dsst_0.pdf
Alday, P. (2022).
Palday/MixedModelsExtras.jl: v0.1.5 [Computer software].
https://doi.org/10.5281/zenodo.7139991
Amt für Statistik. (2021). Primäreinkommen und verfügbares einkommen der privaten haushalte im land brandenburg 1991 bis 2020. Amt für Statistik.
Auguie, B. (2017). Miscellaneous functions for “grid” graphics type, version 2.3 [Computer software].
Bank, W. (2023).
Poverty and inequality platform methodology handbook.
https://datanalytics.worldbank.org/PIP-Methodology/
Bastian, C. C. von, Souza, A. S., & Gade, M. (2016). No evidence for bilingual cognitive advantages: A test of four hypotheses.
Journal of Experimental Psychology: General,
145, 246–258.
https://doi.org/10.1037/xge0000120
Bates, D., Alday, P., Kleinschmidt, D., Calderón, J. B. S., Zhan, L., Bouchet-Valat, M., Noack, A., Arslan, A., Kelman, T., Baldassari, A., Ehinger, B., Karrasch, D., Saba, E., Quinn, J., Hatherly, M., Piibeleht, M., Mogensen, P. K., Babayan, S., & Yakir, L. G. (2023).
JuliaStats/MixedModels.jl: v4.8.2 [Computer software].
https://doi.org/10.5281/zenodo.7529836
Bates, D., Mächler, M., Bolker, B. M., & Walker, S. C. (2015). Fitting linear mixed-effects models using lme4.
Journal of Statistical Software.
https://doi.org/10.18637/jss.v067.i01
Beurskens, R., Muehlbauer, T., & Granacher, U. (2015). Association of dual-task walking performance and leg muscle quality in healthy children.
BMC Pediatrics,
15.
https://doi.org/10.1186/s12887-015-0317-8
Bezanson, J., Edelman, A., Karpinski, S., & Shah, V. B. (2017). Julia: A fresh approach to numerical computing. In
SIAM Review (Vol. 59) [Computer software].
https://doi.org/10.1137/141000671
Bormann, A. (2016). Wissenschaftliche analyse im rahmen der implementierung des einbeinstandtests in der primarstufe im land brandenburg (EMOTIKON-studie). Universität Potsdam.
Bös, K., Worth, A., Opper, E., Oberger, J., Romahn, N., Wagner, M., Jekauc, D., Mess, F., & Woll, A. (2009). Motorik-modul: Eine studie zur motorischen leistungsfähigkeit und körperlich-sportlichen aktivität von kindern und jugendlichen in deutschland. Bundesministerium für Familie, Senioren, Frauen und Jugend.
Clemes, S. A., & Biddle, S. J. H. (2013). The use of pedometers for monitoring physical activity in children and adolescents: Measurement considerations.
Journal of Physical Activity and Health,
10.
https://doi.org/10.1123/jpah.10.2.249
Davidson, M. C., Amso, D., Anderson, L. C., & Diamond, A. (2006). Development of cognitive control and executive functions from 4 to 13 years: Evidence from manipulations of memory, inhibition, and task switching.
Neuropsychologia,
44, 2037–2078.
https://doi.org/10.1016/j.neuropsychologia.2006.02.006
Dubowy, K. O., Baden, W., Bernitzki, S., & Peters, B. (2008). A practical and transferable new protocol for treadmill testing of children and adults.
Cardiology in the Young,
18.
https://doi.org/10.1017/S1047951108003181
Ellert, U., Ravens-Sieberer, U., Erhart, M., & Kurth, B. M. (2011). Determinants of agreement between self-reported and parent-assessed quality of life for children in germany-results of the german health interview and examination survey for children and adolescents (KiGGS).
Health and Quality of Life Outcomes,
9.
https://doi.org/10.1186/1477-7525-9-102
Erhart, M., Ellert, U., Kurth, B. M., & Ravens-Sieberer, U. (2009). Measuring adolescents’ HRQoL via self reports and parent proxy reports: An evaluation of the psychometric properties of both versions of the KINDL-r instrument.
Health and Quality of Life Outcomes,
7.
https://doi.org/10.1186/1477-7525-7-77
Faude, O., Nowacki, P. E., & Urhausen, A. (2004). Comparison of non-invasive tests to assess cardio-respiratory fitness in school children. DEUTSCHE ZEITSCHRIFT FUR SPORTMEDIZIN, 55.
Fernandez-Santos, J. R., Ruiz, J. R., Cohen, D. D., Gonzalez-Montesinos, J. L., & Castro-Piñero, J. (2015). Reliability and validity of tests to assess lower-body muscular power in children.
Journal of Strength and Conditioning Research,
29, 2277–2285.
https://doi.org/10.1519/JSC.0000000000000864
Figura, F., Cama, G., Capranica, L., Guidetti, L., & Pulejo, C. (1991). Asessment of static balance in children. Journal of Sports Medicine and Physical Fitness, 31.
Fjørtoft, I., Pedersen, A. V., Sigmundsson, H., & Vereijken, B. (2011). Measuring physical fitness in children who are 5 to 12 years old with a test battery that is functional and easy to administer.
Physical Therapy,
91, 1087–1095.
https://doi.org/10.2522/ptj.20090350
Fox, J., & Weisberg, S. (2019). An {r} companion to applied regression, third edition. In
Thousand Oaks CA: Sage. [Computer software].
https://CRAN.R-project.org/package=flextable
Fühner, T., Granacher, U., Golle, K., & Kliegl, R. (2021). Age and sex effects in physical fitness components of 108,295 third graders including 515 primary schools and 9 cohorts.
Scientific Reports,
11.
https://doi.org/10.1038/s41598-021-97000-4
Fühner, T., Granacher, U., Golle, K., & Kliegl, R. (2022). Effect of timing of school enrollment on physical fitness in third graders. Nature - Scientific Reports, 12.
Gerodimos, V. (2012). Reliability of handgrip strength test in basketball players.
Journal of Human Kinetics,
31.
https://doi.org/10.2478/v10078-012-0003-y
Gohel, D. (2022). Officer: Manipulation of microsoft word and PowerPoint documents, version 0.4.4 [Computer software].
Gohel, D., & Skintzos, P. (2022). Flextable: Functions for tabular reporting, version 0.8.3 [Computer software].
Golle, K. (2015). Physical fitness in school-aged children. University of Potsdam.
Golle, K., Muehlbauer, T., Wick, D., & Granacher, U. (2015). Physical fitness percentiles of german children aged 9-12 years: Findings from a longitudinal study.
PLoS ONE,
10.
https://doi.org/10.1371/journal.pone.0142393
Goyder, J., Warriner, K., & Miller, S. (2002). Evaluating socio-economic status (SES) bias in survey nonresponse. Journal of Official Statistics, 18.
Granacher, U., & Golle, K. (2016). Generierung von normwerten und die prüfung der reliabilität des einbeinstands- und standweitsprungtests. Universität Potsdam.
Haaren, B. von, Härtel, S., Seidel, I., Schlenker, L., & Bös, K. (2011). Validity of a 6-min endurance run and a 20-m shuttle run in 9- to 11-year old children. Deutsche Zeitschrift Fur Sportmedizin, 62.
Hohenstein, S., & Kliegl, R. (2022).
Remef: Remove partial effects, version 1.0.7 [Computer software].
https://github.com/hohenstein/remef/
Jekauc, D., Reimers, A. K., Wagner, M. O., & Woll, A. (2013). Physical activity in sports clubs of children and adolescents in germany: Results from a nationwide representative survey.
Journal of Public Health (Germany),
21.
https://doi.org/10.1007/s10389-013-0579-2
KMK. (1999). Grundsätze für die durchführung von sportförderunterricht sowie für die ausbildung und prüfung zum erwerb der befähigung für das erteilen von sportförderunterricht. Kultusministerkonferenz.
Lampert, T., Müters, S., Stolzenberg, H., & Kroll, L. E. (2014). Messung des sozioökonomischen status in der KiGGS-studie: Erste folgebefragung (KiGGS welle 1).
Bundesgesundheitsblatt - Gesundheitsforschung - Gesundheitsschutz,
57.
https://doi.org/10.1007/s00103-014-1974-8
Lawrenz, W., & Stemper, T. (2012). Comparison of 6-minute-jog-walk and maximal oxygen uptake in 8-10-year old school children. DEUTSCHE ZEITSCHRIFT FUR SPORTMEDIZIN, 63.
Lüdecke, D. (2021). sjPlot: Data visualization for statistics in social science, r package version version 2.8.12.
Lüdecke, D., Ben-Shachar, M., Patil, I., Waggoner, P., & Makowski, D. (2021). Performance: An r package for assessment, comparison and testing of statistical models.
Journal of Open Source Software,
6.
https://doi.org/10.21105/joss.03139
MBJS. (2011). Handreichung sport - empfehlung zur umsetzung - sportförderunterricht. Ministerium für Bildung, Jugend und Sport - Brandenburg.
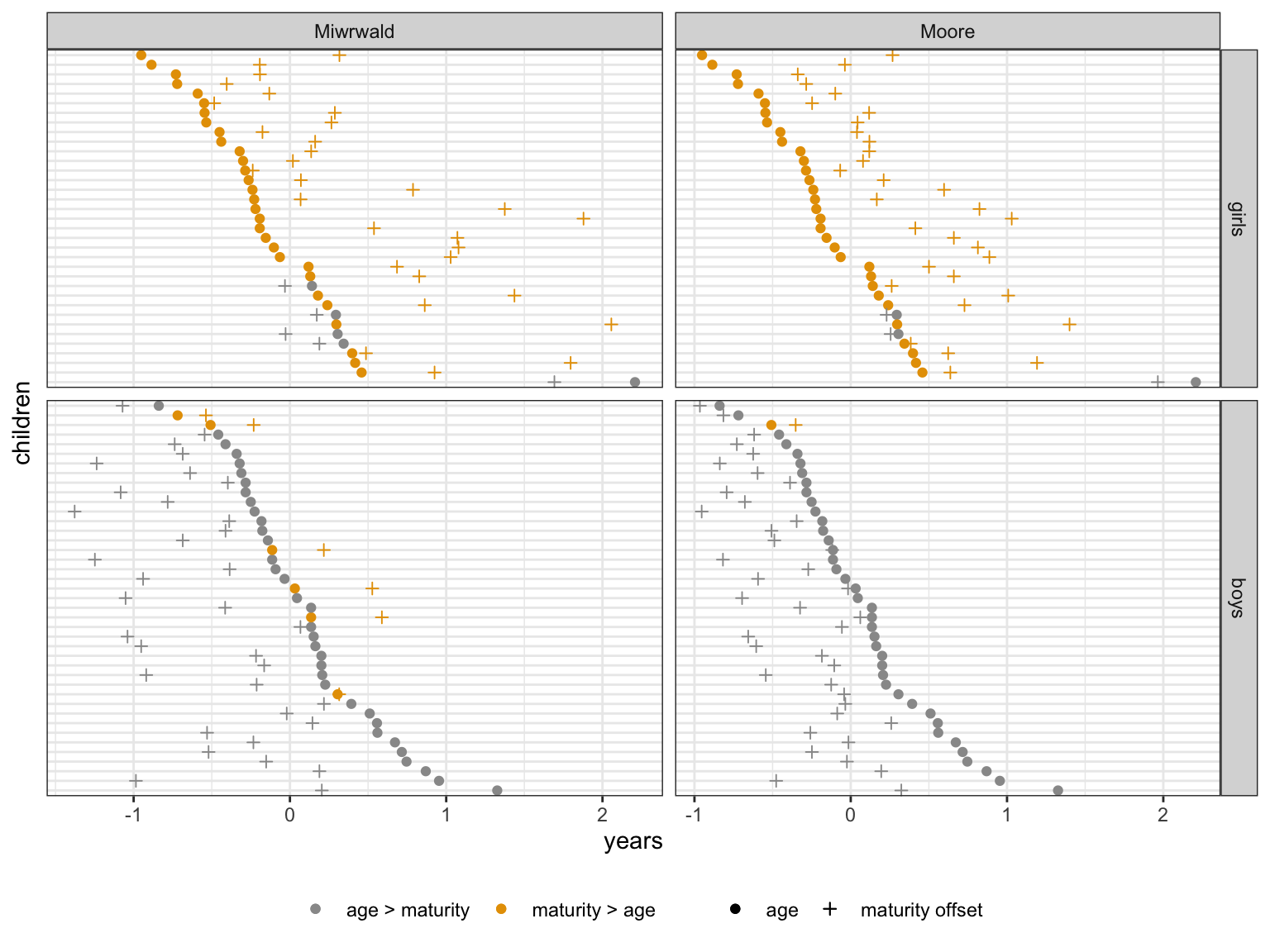
Mirwald, R. L., Baxter-Jones, A. D. G., Bailey, D. A., & Beunen, G. P. (2002). An assessment of maturity from anthropometric measurements.
Medicine and Science in Sports and Exercise,
34, 689–694.
https://doi.org/10.1249/00005768-200204000-00020
Moore, S. A., McKay, H. A., Macdonald, H., Nettlefold, L., Baxter-Jones, A. D. G., Cameron, N., & Brasher, P. M. A. (2015). Enhancing a somatic maturity prediction model.
Medicine and Science in Sports and Exercise,
47.
https://doi.org/10.1249/MSS.0000000000000588
Petermann, F., & Petermann, U. (2011). Wechsler intelligence scale for children® – fourth edition - manual 1: Grundlagen, testauswertung und interpretation. Pearson Assessment & Information GmbH.
R Core Team. (2022). R: The r project for statistical computing [Computer software].
Ravens-Sieberer, U., Ellert, U., & Erhart, M. (2007). Gesundheitsbezogene lebensqualität von kindern und jugendlichen in deutschland.
Bundesgesundheitsblatt - Gesundheitsforschung - Gesundheitsschutz,
50.
https://doi.org/10.1007/s00103-007-0244-4
Reitan, R. (2004). The trail making test as an initial screening procedure for neuropsychological impairment in older children.
Archives of Clinical Neuropsychology,
19, 281–288.
https://doi.org/10.1016/S0887-6177(03)00042-8
Reitan, R. M. (1971). Trail making test results for normal and brain-damaged children.
Perceptual and Motor Skills,
33, 575–581.
https://doi.org/10.2466/pms.1971.33.2.575
Reitan, R. M., & Wolfson, D. (1995). Category test and trail making test as measures of frontal lobe functions.
The Clinical Neuropsychologist,
9.
https://doi.org/10.1080/13854049508402057
Schmidt, S., Will, N., Henn, A., Reimers, A., & Woll, A. (2016). Der motorik-modul aktivitätsfragebogen MoMo-AFB - leitfaden zur anwendung und auswertung (K. Bös, A. Worth, & A. Woll, Eds.). Karlsruher Institut für Technologie.
Schulz, S. (2013). The reliability of the star co-ordination run and the 1-kg medicine ball push–physical fitness tests used in the EMOTIKON-study. University Potsdam.
Simon, J. R., & Rudell, A. P. (1967). Auditory s-r compatibility: The effect of an irrelevant cue on information processing.
Journal of Applied Psychology,
51, 300–304.
https://doi.org/10.1037/h0020586
Venables, W. N., & Ripley, B. D. (2002). Modern applied statistics with s fourth edition by. In World (4th ed., Vol. 53).
Wickham, H. (2016). ggplot2 - elegant graphics for data analysis. In Springer-Verlag New York [Computer software].
Wickham, H., Averick, M., Bryan, J., Chang, W., McGowan, L., François, R., Grolemund, G., Hayes, A., Henry, L., Hester, J., Kuhn, M., Pedersen, T., Miller, E., Bache, S., Müller, K., Ooms, J., Robinson, D., Seidel, D., Spinu, V., … Yutani, H. (2019). Welcome to the tidyverse.
Journal of Open Source Software,
4.
https://doi.org/10.21105/joss.01686
Willis, K. (2020). Theories and practices of development. In
Theories and Practices of Development.
https://doi.org/10.4324/9781315559469
Wind, A. E., Takken, T., Helders, P. J. M., & Engelbert, R. H. H. (2010). Is grip strength a predictor for total muscle strength in healthy children, adolescents, and young adults?
European Journal of Pediatrics,
169.
https://doi.org/10.1007/s00431-009-1010-4